Fermat's Christmas Theorem

I'm going to present what I think is a cool proof of the following theorem (original pdf version):

Theorem: An odd prime $p$ can be expressed as

$$p = x^2 + y^2$$

with $x, y$ integers if $p \equiv 1 \mod 4$

Example: $5 = 1^2 + 2^2$, $13 = 2^2 + 3^2$, $17 = 1^2 + 4^2$, $29 = 2^2 + 5^2$

Setup

Lemma 1: For every $a$ where $p \nmid a$ there exists $b$ such that $ab \equiv 1 \mod p$

Example: For $a = 2$ and $p = 5$ we may choose $b = 3$.

Proof by Bézout’s theorem: Since $a$ and $p$ are coprime there exists integer $n$ and $M$ such that $an + pm = 1$ hence $an \equiv 1 \mod p$. :)

Lemma 2: For all prime numbers $p$, $(p-1)! \equiv -1 \mod p$.

Example: $1 \cdot 2 \cdot 3 \cdot 4 \equiv 1 \cdot (2 \cdot 3) \cdot (\minus 1) \mod 5$

Example: $$\begin{align*} &1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot 10 \cdot 11 \cdot 12 \\ \equiv_{13} \quad & 1 \cdot (2\cdot7)\cdot(3\cdot9)\cdot(4\cdot10)\cdot(5\cdot8)\cdot (6\cdot11)\cdot(-1) \end{align*}$$

Something fishy is going on, every pair of numbers I put in brackets multiples to something $1 \mod 13$. We can pair everything up with something else and have those multiply to $1$ besides $1$ and $-1$. Leaving $1 \cdot 1 \cdot 1 \cdots 1 \cdot (-1)$. So $12! \equiv 1 \mod 13$

Proof by pairing: Every number from $1$ to $𝑝 − 1$ is coprime to $𝑝$ and hence pairs uniquely to some other number from $1$ to $𝑝 − 1$ to multiply to $1$. Unique because $𝑎𝑏 ≡1≡𝑎𝑐$ implies $𝑎(𝑏 −𝑐) ≡ 0$ and hence $𝑝 ∣ 0$ or $𝑝 ∣ 𝑏 −𝑐$ neither of which can be true. The only two numbers which pair with themselves are $𝑥$ where $𝑥^2 ≡ 1$ hence $(𝑥 −1)(𝑥 +1) ≡ 0$ and so $𝑥 ≡ ±1 \mod 𝑝$. The rest is trivial, you can do it yourself.

Lemma 3: For a prime number $p \equiv 1 \mod 4$ , there exists $n$ such that

$$n^2 \equiv -1 \mod p$$

Proof: Let $p = 4k + 1$ and consider $n \equiv 1 \cdot 2 \cdot 2 \cdots {2k}$. $$\begin{align*} n^2 & \equiv_p 1 \cdot 2 \cdots (2k) \cdots (2k+1) \cdots (4k-2) \cdot (4k-1) \\ & \equiv (-1)^{2k} \cdot 1 \cdot 2 \cdots (2k) \cdot (2k+1) \cdots (4k-2) \cdot (4k-1) \\ & \equiv (-1)^{2k} (p-1)! \\ & \equiv (p-1)! \\ & \equiv (-1) \end{align*}$$

Minkowski’s Theorem

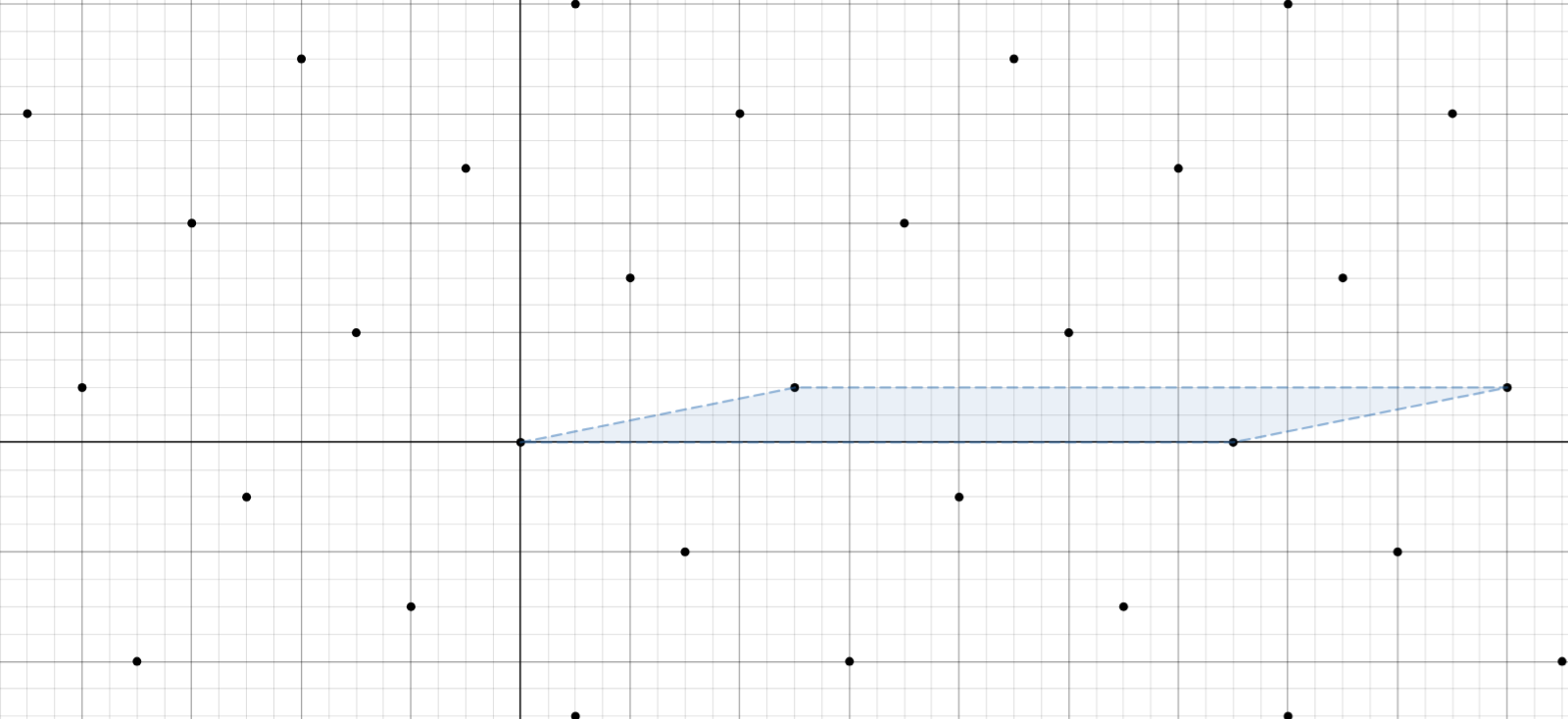
A lattice of points generated by $n$ linearly independent vectors $v_1, v_2, \dots, v_n$ is the set of all points of the form

$$a_1 v_1 + a_2 v_2 + \dots + a_n v_n$$

where $a_1, a_2, \dots, a_n$ are integers.

Minkowski’s Theorem: If a convex set in $\mathbb{R}^n$ is symmetric about the origin and has volume $2^n$ times the volume of the fundamental parallelepiped of a lattice in $\mathbb{R}^n$, then the set contains a non-zero point of the lattice.

What this is really saying is that if you have a lattice of points in $\mathbb{R}^n$ and you blow a big enough balloon about the origin, you will eventually hit a lattice point. More specifically in the case of $\mathbb{R}^2$, if you have a lattice of points generated by two vectors $v_1$ and $v_2$ and you draw a circle with area of $4 \cdot \text{area}(v_1,v_2)$ centered at the origin, then there must be a lattice point other than the origin inside that circle.

Conclusion

Proof of Fermat’s Christmas Theorem: Consider the lattice of points generated by the two vectors $\begin{pmatrix} n \\ 1 \end{pmatrix}$ and $\begin{pmatrix} 0 \\p \end{pmatrix}$. The area of the parallelogram spanned by these two vectors is $p$. What’s important is that every lattice point $(x,y)$ is such that $x^2 + y^2 \equiv 0 \mod p$.

Now draw a circle of radius $\sqrt{\frac{4p}{\pi}}$ centered at the origin. The area of this circle is $4p$ and so by Minkowski’s Theorem there must be a lattice point $(x,y)$ inside this circle other than the origin.

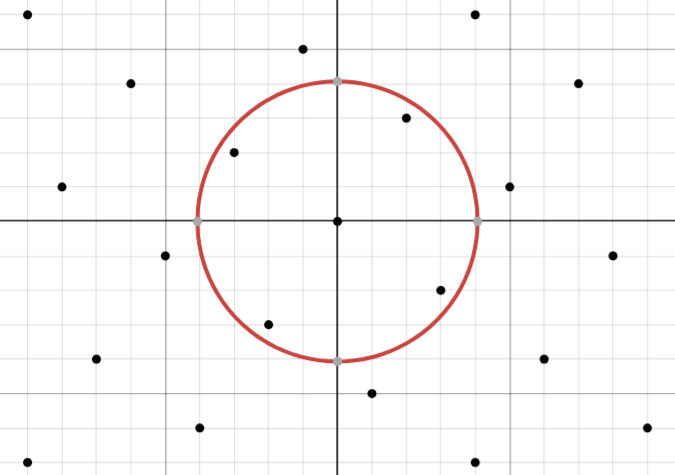
$p \mid x^2 + y^2$ and $x^2 + y^2 < \frac{4 p} \pi$. So $x^2 + y^2 = p$ . So there must exist integers $x$ and $y$ such that $p = x^2 + y^2$.